9. Line Integrals

Homework

1. A wire has the shape of the parametric curve \(\vec r(t)=\left\langle\dfrac{1}{2}t^2+1,t-2,\dfrac{2\sqrt{2}}{3}t^{3/2}\right\rangle\) from \(t=0\) to \(t=4\) with linear mass density \(\delta=y+2\).

   1. Find the length of the wire.

   2. Find the total mass.

   3. Find the \(y\)-component of the center of mass.

   4. Find the average value of the function \(f(x,y,z)=(x-1)(y+2)\).

2. Compute the integral \(\displaystyle \int_{(0,0,0)}^{(1,\sqrt{3/2\,},1)} xz\,ds\) along the twisted cubic \(\vec r(t)=\left(t,\sqrt{\dfrac{3}{2}}t^2,t^3\right)\).

3. Find the mass of the cusp \(x^3=y^2\) for \(0 \le x \le \dfrac{1}{9}\) if the linear density is \(\delta=x\). The cusp may be parametrized as \(\vec r(t)=(t^2,t^3)\).

4. Find the work done by the force \(\vec F=\langle 2z^2,2yz,5xz\rangle\) on an object which moves along the curve \(\vec r=(t^3,t^2,t)\) between \(P=(1,1,1)\) and \(Q=(8,4,2)\).

5. Compute \(\displaystyle \int_{(0,4,0)}^{(6\pi,4,0)} \left[\rule{0pt}{10pt}(y+z)\,dx+z\,dy-y\,dz\right]\) along the helix \(\vec r=\langle3t, 4\cos(2t), 4\sin(2t)\rangle\).

6. Find the flow of the velocity field \(\vec V=(2xz,xy,-4y)\) along the twisted cubic \(\vec r(t)=(t,t^2,t^3)\) from \((1,1,1)\) to \((2,4,8)\). Is the fluid flowing in the same or opposite direction as the curve is traversed?

7. Find the circulation of the velocity field \(\vec V=(-y^3,xy^2)\) counterclockwise around the circle \(x^2+y^2=4\). Does the fluid flow clockwise or counterclockwise?

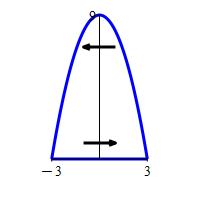
8. Find the circulation of the magnetic field \(\vec B=(x^2,x+y,0)\) counterclockwise along the line segment \(y=0\) from \(x=-3\) to \(x=3\) and around the parabola \(y=9-x^2\) from \(x=3\) to \(x=-3\). Does the magnetic field circulate clockwise or counterclockwise?